Logarithmic spiral

Cutaway of a nautilus shell showing the chambers arranged in an approximately logarithmic spiral. The plotted spiral (dashed blue curve) is based on growth rate parameter b = 0.1759

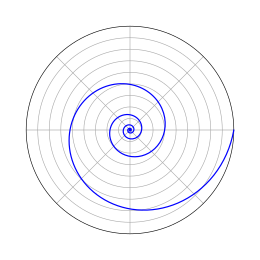
A logarithmic spiral, equiangular spiral or growth spiral is a self-similar spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral".

         Logarithmic spiral (pitch 10°)

Logarithmic spirals in nature

In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follows some examples and reasons:

• The approach of a hawk to its prey. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
• The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the sun (or moon for nocturnal species) is the only light source and flying that way will result in a practically straight line. 
• The arms of spiral galaxies. Our own galaxy, the Milky Way, has several spiral arms, each of which is roughly a logarithmic spiral with pitch of about 12 degrees. 
• The nerves of the cornea (this is, corneal nerves of the subepithelial layer terminate near superficial epithelial layer of the cornea in a logarithmic spiral pattern). 
• The bands of tropical cyclones, such as hurricanes.
• Many biological structures including the shells of mollusks. In these cases, the reason may be construction from expanding similar shapes, as shown for polygonal figures in the accompanying graphic.

Logarithmic spiral beaches can form as the result of wave refraction and diffraction by the coast. Half Moon Bay (California) is an example of such a type of beach.

Some of my drawings where spirals were noted:

Thanks to Mark for bringing up this subject. I think another reason why seashells are so attractive and relaxing is they often follow algorithmic spiral or fractals-type self-similar curves. This pattern is found throughout the natural world and so it probably ties in with our deep sense of organic connection with the natural world. I would like to research on the therapeutic impact of spirals and curves. Can there be a truth behind this fact that connects to the feeling of comfort?